graph LR
A[用户ID] --> B(哈希函数)
B --> C[256位哈希值]
C --> D{取模运算}
D --> E[分组编号]
E --> F[实验分组]
3 ABTest
3.1 概览
本章介绍AB测试。AB测试(也称为随机对照试验 - RCT, Randomized Controlled Trial)是一种用于因果推断的实验设计方法。其核心在于通过随机分配将受试单元(用户、会话、页面访问等)分配到不同的处理组(通常是A:对照组/Baseline,B:新方案组),在控制其他变量(通过随机化)的前提下,比较不同处理对特定目标指标的影响,从而决定哪个更优。
3.2 本章参考资料点击这里查看。
3.3 理论基础
3.3.1 因果推断的基石:潜在结果框架与随机化
潜在结果框架(Neyman-Rubin Causal Model):
定义:对于每个实验单元\(i\)(用户、会话等),定义两个潜在结果:
\(Y_i(1)\):单元\(i\)接受处理\(B\)(干预)时的结果
\(Y_i(0)\):单元\(i\)接受处理\(A\)(对照)时的结果
个体处理效应:\(\text{ITE} = \tau_i = Y_i(1) - Y_i(0)\)
根本问题:对于任何单元\(i\),我们只能观察到\(Y_i(1)\)或\(Y_i(0)\),永远无法同时观测两者,观察到的结果\(Y_i^{obs} = Z_i * Y_i(1) + (1 - Z_i) * Y_i(0)\),其中\(Z_i\)是指示变量,\(Z_i=1\) 表示分配到\(B\)组,\(Z_i=0\) 表示分配到\(A\)组)。
目标:估计平均处理效应\(\text{ATE} = \tau = E[\tau_i] = E[Y_i(1)-Y_i(0)]=E[Y(1)]-E[Y(0)]\)
随机化
关键假设(Ignorability/Unconfoundedness):通过完全随机分配,我们确保处理分配\(Z_i\)独立于潜在结果,即\(Y_i(1),Y_i(0) \perp Z_i\),这意味着\(E[Y_i(1) | Z_i=1] = E[Y_i(1) | Z_i=0] = E[Y_i(1)]\)(同理于\(Y_i(0)\))。
无偏估计量:基于观测数据,ATE 的一个简单无偏估计量是组间均值差\[\hat{τ}_{DiM} = \hat{E}[Y^{obs} | Z=1] - \hat{E}[Y^{obs} | Z=0] = \bar{Y}_B - \bar{Y}_A\]
证明无偏性: \[E[\hat{τ}_{DiM}] = E[\bar{Y}_B - \bar{Y}_A] = E[\bar{Y}_B] - E[\bar{Y}_A] = E[Y(1) | Z=1] - E[Y(0) | Z=0]\](根据观测数据定义)
由于随机化(\(Y_i(1),Y_i(0) \perp Z_i\)),有\(E[Y(1) | Z=1] = E[Y(1)]\)且\(E[Y(0) | Z=0] = E[Y(0)]\) 因此\(E[\hat{τ}_{DiM}] = E[Y(1)] - E[Y(0)] = ATE\)
协变量平衡 (Covariate Balance): 随机化也确保所有观测到的\(X\) 和未观测到的 \(U\) 混杂因素(Confounders)在组间的分布是相同的(渐近意义上): \(F(X | Z=1) = F(X | Z=0)\)和\(F(U | Z=1) = F(U | Z=0)\)
这是实现\(Y(1),Y(0) \perp Z\)的关键保障。AA测试检查的就是观测到的 X是否平衡。
3.3.2 假说检验
- 核心框架
原假设\(H_0\):\(ATE = 0\)或等价的\(\mu_A = \mu_B\)(总体均值相等)或\(p_A = p_B\)(总体比例相等)。
备择假设\(H_1\):\(ATE \neq 0\)(双尾)或\(ATE>0\)或\(ATE<0\)(单尾)。
检验统计量\(T\):构造一个统计量,其分布在\(H_0\)成立时已知(或渐进已知)。
\(P-value\):\(p=P\left(|T| \geq \left|t_{obs}\right| \middle| H_0\right)\),即\(H_0\)成立时,观察到当前统计量\(t_{obs}\)甚至于更极端值的概率。
决策:若\(p<\alpha\),\(\alpha\)为我们预设的显著性水平,则拒绝\(H_0\)。
- 连续性指标:双样本\(t\)检验
例如平均订单金额、会话时长。
假设:
独立性Independent Samples
正态性Normality:每组数据近似正态分布(或样本量足够大,依赖CLT)
方差齐性Homoscedasticity:\(\sigma_A^2 = \sigma_B^2 = \sigma^2\)
检验统计量:
\[t = \frac{(\bar{Y}_B - \bar{Y}_A) - 0}{s_p \sqrt{\frac{1}{n_A} + \frac{1}{n_B}}}\] 其中\(s_p² = \frac{(n_A - 1)s_A² + (n_B - 1)s_B²}{n_A + n_B - 2}\)是合并方差估计量 (Pooled Variance Estimator),\(s_A^2\),\(s_B^2\)是样本方差,\(n_A\),\(n_B\)是样本量。
分布:在\(H_0\)和假设成立的条件下,\(t \sim t_{df}\),自由度\(df = n_A+n_B-2\)
方差不齐 (Welch’s t-test):若方差不齐,使用调整后的统计量和自由度, \[t = \frac{\bar{Y}_B - \bar{Y}_A}{\sqrt{\frac{s_A²}{n_A} + \frac{s_B²}{n_B}}}\],自由度为\(df ≈ \frac{(\frac{s_A²}{n_A} + \frac{s_B²}{n_B})²}{\frac{(s_A²/n_A)²}{n_A - 1} + \frac{(s_B²/n_B)²}{n_B - 1}}\)
- 比例型指标:双样本比例检验(\(Z\)检验)
例如点击率、转化率。
假设:
独立性
大样本:\((n_A p_A > 5, n_A (1-p_A) > 5, n_B p_B > 5, n_B (1-p_B) > 5)\),确保二项分布近似正态。
检验统计量(基于合并比例): \[Z = \frac{\hat{p}_B - \hat{p}_A}{\sqrt{\hat{p}(1-\hat{p}) (\frac{1}{n_A} + \frac{1}{n_B})}}\] 其中\(\hat{p} = \frac{X_A + X_B}{n_A + n_B}\),\(X_A\),\(X_B\)是成功的次数,是\(H_0(p_A =p_B = p)\)下\(p\)的合并估计量。
分布:在\(H_0\)和假设成立的条件下,\(Z\sim N(0, 1)\)(渐近)。
基于独立方差(更常用且推荐):
\[Z = \frac{\hat{p}_B - \hat{p}_A}{\sqrt{\hat{p}(1-\hat{p}) (\frac{1}{n_A} + \frac{1}{n_B})}}\],这个版本不依赖与\(H_0\)下\(p_A=p_B\)的假设,在构建置信区间时更加自然,检验功效稍低但是更稳健。渐近分布同样是\(N(0, 1)\)。
计数型指标 例如人均点击次数。常假设服从泊松分布,使用基于泊松回归或负二项回归的检验(处理过离散问题)。
置信区间(CI)
概念:基于样本数据构造一个区间\((L, U)\),使得我们要估计的参数\(\theta\)(我们这里是\(ATE\))落在这个区间的概率是\(1-\alpha\),即\(P(L\leq \theta \leq U) = 1-\alpha\)。频率学派的解释是,重复多次试验,每次构造一个CI,那么大约\(1-\alpha\)的CI会包含真实的\(\theta\)。以下均以双尾检验为例。
连续性指标(差异): \[(\bar{Y}_B - \bar{Y}_A) \pm t_{df, 1-\alpha/2} \times SE(\bar{Y}_B - \bar{Y}_A)\] 其中 \(SE(\bar{Y}\_B - \bar{Y}\_A) = \sqrt{\frac{s_A²}{n_A} + \frac{s_B²}{n_B}}\)(Welch))或\(s_p \sqrt{\frac{1}{n_A} + \frac{1}{n_B}}\)(Pooled)。
比例型指标(差异):\[(\hat{p}_B - \hat{p}_A) \pm Z_{1-\alpha/2} \times \sqrt{\frac{\hat{p}_A(1-\hat{p}_A)}{n_A} + \frac{\hat{p}_B(1-\hat{p}_B)}{n_B}}\]
解读:如果95%CI不包含0,则双尾验证在$$显著性水平下显著。CI宽度反映了估计的精确度。
3.3.3 统计功效与样本量计算
- 定义与公式
I类错误(\(\alpha\)):\(H_0\)为真时,错误地拒绝\(H_0\)。也就是说宣称有差异实际没有。
II类错误(\(\beta\)):\(H_1\)为真时,没有拒绝\(H_0\)。也就是说实际上有差异但是没有检测到。
功效(Power)\(1-\beta\):\(P(\text{Reject } H₀ | H₁ \text{ is true})\)。即当真实效应\(\delta = |ATE|\)(或\(|\mu_B -\mu_A|\),\(|p_B - p_A|\))存在且等于最小期望检测效应(MDE)时,正确拒绝\(H_0\)的概率。换句话说,就是当处理B确实比A好(\(H_1\)为真)时,正确拒绝\(H_0\)的概率\(1-\beta\)。
影响功效的关键因素(以双样本\(t\)检验为例):
效应量(\(\delta\)):期望检测到的最小有意义的差异\(\delta = \frac{|\mu_B - \mu_A|}{\sigma}\),这是标准化效应量,Cohen’sd。\(\delta\)越大,功效越高,\(\delta\)越小,检测所需要的样本量越大。
样本量(\(n = n_A= n_B\)):\(n\)越大,功效越高,功效\(\propto \sqrt{n}\)
显著性水平(\(\alpha\)):犯I类错误(假阳性)的概率。\(\alpha\)越大,即允许更多假阳性,功效越高。\(\alpha\)越小,所需要样本量越大。
方差(\(\sigma^2\)):\(\sigma^2\)越大,功效越低。指标本身的变异性越大,检测相同效应量所需的样本量越大(对于连续型指标)。
基准比率(\(p_A\)):对于比例指标,基准转化率影响方差(p(1-p)),在p=0.5时最大。
样本量计算公式(双样本\(t\)检验,双尾,等样本量):
\[n \approx \frac{2 (Z_{1-\alpha/2} + Z_{1-\beta})^2 \sigma^2}{\delta^2}\]
其中\(Z_{1-\alpha/2},Z_{1-\beta}\)是标准正态分布的分位数,\(\delta\)是未标准化的效应量(\(|\mu_B-\mu_A|\))。这个公式推导基于\(H_0\)下的统计量\(\sim N(0, 1)\),\(H_1\)下的统计量\(\sim N(\frac{\delta}{\sigma \sqrt{2/n}}, 1)\),令两个分布的拒绝域边界相交即可解出\(n\)。
- 比例型指标(双样本比例检验,双尾,等样本量):
\[n \approx \frac{ (Z_{1-\alpha/2} \sqrt{2\bar{p}(1-\bar{p})} + Z_{1-\beta} \sqrt{p_A(1-p_A) + p_B(1-p_B)} )² }{\delta²}\] 其中\(\delta = |p_B-p_A|,\bar{p} = \frac{p_A+p_B}{2}\),推导类似,考虑\(H_0\)下方差基于\(\bar{p}\),\(H1\)下方差基于真实的\(p_A\)和\(p_B\)。
3.3.4 方差估计的挑战(用户级随机化)
问题核心:在用户级随机化的AB测试中,分析单元(如页面浏览PV,点击Click)与随机化单元(用户User)不一致。同一个用户的不同事件/行为不独立。
后果:传统的方差估计公式(如\(\frac{s^2}{n}\))会严重低估真实方差,导致:
CI过窄
\(p-value\)过小,I类错误率(假阳性率)膨胀
数学解释:
假设有\(m\)个用户\(i = 1...m\),用户\(i\)贡献\(n_i\)个观测值(如\(PV\)),总观测值\(N = \sum_i n_i\)
核心指标\(Y\)在用户\(i\)上的平均为\(\bar{Y}_i\)
组件差异估计量\(\hat{\tau} = \bar{Y}_B - \bar{Y}_A\)
其真实方差为:\(Var(\hat{τ}) = Var(\frac{1}{m_B} \sum_{i \in B} \bar{Y}_i - \frac{1}{m_A} \sum_{j \in A} \bar{Y}_j)\),由于用户间是独立的,\(Var(\hat{τ}) = \frac{Var(\bar{Y}_i | B)}{m_B} + \frac{Var(\bar{Y}_j | A)}{m_A}\)
而传统方差估计(假设观测独立)为:\(\widehat{Var}_{naive}(\hat{τ}) \approx \frac{s_B²}{N_B} + \frac{s_A²}{N_A}\),其中\(N_B = \sum_{i \in B} n_i\)(B组总观测数),\(s_B^2\)是基于所有B组观测值计算的方差
\(\widehat{Var}_{naive}\)会系统性小于\(Var(\hat{\tau})\),因为忽略了用户的内相关性。低估的程度取决于用户内相关性的强度和用户行为次数\(n_i\)的变异度。
解决方案:
\(Delta\) \(Method\):推倒\(\hat{\tau}\)方差的理论表达式并进行估计。适用于特定指标类型(如人均指标)。
聚类标准误(Cluster-Robust Standard Errors - CRSE):将方差估计建立在随机化单元(用户)的层面。
将每一个用户视为一个“聚类”
计算每个用户\(i\)对\(\hat{\tau}\)的“得分”(Influence Function)或残差贡献\(e_i\)
聚类标准误为: \(\widehat{Var}_{CR}(\hat{τ}) = \frac{m}{m-1} \frac{m}{m_A m_B} \sum_{i=1}^m (\tilde{e}_i - \bar{\tilde{e}})^2\),其中\(\tilde{e}_i\)是用户\(i\)的聚合残差贡献(具体形式取决于模型)。这是最常用且稳健的方法。
Booststrap(聚类Booststrap):对用户进行重抽样(而不是对观测值),保持用户的所有数据完整。每次重抽样后计算\(\hat{\tau}\),用多次(B次)重抽样得到的\(\hat{\tau}^{(b)}\)的方差来估计\(\hat{\tau}\)。计算量大但是灵活。
3.3.5 多重检验问题(Multiple Testing Problem)
问题核心:同时进行\(K\)次独立的假设检验,每个检验的显著性水平都为\(\alpha\)。那么至少出现一次假阳性(I类错误)的概率(族系错误率FWER,Family-Wise Error Rate)是\[FWER = P(\text{至少一个错误拒绝} | \text{所有 } H₀ \text{ 为真}) = 1 - (1 - α)^K ≈ Kα \quad (\text{当 } α \text{ 很小时})\],即使\(\alpha = 0.05\),当\(K\)为10时,FWER约为0.4,假阳性率非常高。
ABTest中的来源:
同时测试多个核心指标(\(K>1\))
同时测试多个变体(A/B/C/D…测试,\(K>1\)个比较)
数据窥探(Peeking):在实验运行期间多次查看结果并进行检验。每次查看都是一次独立的检验机会(\(K\)很大)。
控制方法(待补充)
3.3.6 进阶统计视角(待补充)
AB测试的统计学原理深植于因果推断的潜在结果框架,随机化是其无偏估计的基石。假设检验 (t/Z检验)提供决策依据,置信区间量化不确定性。功效分析确保实验可靠性,样本量计算是实验设计的核心。实践中必须警惕方差低估 (用户级相关性) 和多重检验膨胀,采用聚类标准误或校正方法。贝叶斯方法和序贯检验提供了替代视角和效率提升。理解异质性效应能挖掘更深价值。掌握这些原理,是设计和解读可靠AB测试的关键。
3.3.7 哈希算法
数学本质 :单向函数映射:\(h: \{0,1\}^* \rightarrow \{0,1\}^n\)
输入:任意长度的数据(用户ID,设备ID)
输出:固定长度摘要(128-256位)
核心特征:
确定性:相同输入 \(\rightarrow\) 相同输出
雪崩效应:1bit变化 \(\rightarrow\) >50%输出位变化
抗碰撞性:极难找到不同输入同输出
业务视角的哈希过程
AB测试中的关键哈希算法
- 经典算法对比
| 算法 | 输出长度 | 业务适用场景 | 性能(1M操作/秒) |
|---|---|---|---|
| MD5 | 128位 | 淘汰中(安全风险) | 550 |
| SHA-1 | 160位 | 兼容旧系统 | 450 |
| SHA-256 | 256位 | 主流AB测试平台 | 220 |
| MurmurHash3 | 128位 | 高性能实时分流 | 850 |
- 分层哈希设计
import hashlib
def assign_group(user_id: str,
salt: str,
layers: dict) -> dict:
"""
用户多实验层分配
:param user_id: 用户唯一标识
:param salt: 实验层盐值
:param layers: 实验层配置
{层1: {分组数: 3}, 层2: {分组数: 2}}
:return: {层1: 组A, 层2: 组B}
"""
assignments = {}
for layer_name, config in layers.items():
# 层专属盐值 = 全局盐值 + 层名
layer_salt = salt + layer_name
# 计算哈希摘要
hash_hex = hashlib.sha256((user_id + layer_salt).encode()).hexdigest()
# 转换为整数
hash_int = int(hash_hex[:16], 16) # 取前16字符足够
# 取模分组
group_idx = hash_int % config['group_count']
assignments[layer_name] = f"组{chr(65+group_idx)}"
return assignments
# 示例调用
user_group = assign_group(
user_id="u_1234567",
salt="2023Q3_EXP",
layers={
"UI改版层": {"group_count": 3},
"推荐算法层": {"group_count": 2}
}
)
print(user_group) {'UI改版层': '组C', '推荐算法层': '组B'}业务场景应用详解
- 1.流量分桶机制
graph TD
A[总流量] --> B[桶1:0-999]
A --> C[桶2:1000-1999]
A --> D[...]
A --> E[桶N:9000-9999]
B -->|10%| F[实验A对照组]
B -->|15%| G[实验A策略组]
B -->|5%| H[实验B测试组]
C --> I[...]
业务规则:
每个桶包含1000个槽位(0-999)
用户ID哈希后取模10000\(\rightarrow\)分配桶号
实验配置定义桶范围到分组的映射
2.一致性保障策略
问题场景:用户多次访问应保持相同分组
解决方案:\(\text{分组ID} = \text{hash}(\text{用户ID} + \text{实验盐值}) \mod K\),其中实验盐值=实验ID+版本号;版本更新时盐值会变化,需要重新分组
- 3.样本均衡技术——分层哈希(Stratified Hashing)
import hashlib
def stratified_hash(user_id, strata):
"""
基于用户特征分层哈希
:param strata: 分层特征值(如"new_user")
"""
base_hash = hashlib.sha256(user_id.encode()).hexdigest()
# 特征值影响低比特位
strata_hash = hashlib.sha256((base_hash + strata).encode()).hexdigest()
return int(strata_hash, 16) % 1000生产环境最佳实践
- 盐值管理规范
| 盐值类型 | 生成规则 | 变更时机 | 业务影响 |
|---|---|---|---|
| 实验盐 | 实验ID + 创建时间戳 | 实验重建时 | 用户重新分组 |
| 全局盐 | 季度编号 + 密钥轮换版本 | 每季度轮换 | 所有实验重新分组 |
| 层盐 | 实验盐 + 层名哈希 | 层配置修改时 | 该层用户重新分组 |
- 分流诊断异常矩阵
| 症状 | 可能原因 | 验证方法 | 解决方案 |
|---|---|---|---|
| 分组比例偏差 > 5% | 取模基数非质数 | 检查分组数是否为素数 | 改用质数分组 |
| 新用户集中特定组 | 用户ID生成规则有偏 | 卡方检验不同ID段分布 | 增加哈希值混合 |
| 实验组指标周期性震荡 | 时间戳参与哈希计算 | 移除时间相关因子 | 固定盐值 + 用户ID |
| 移动/PC用户分组不一致 | 设备类型未纳入分层 | 分平台验证分布均匀性 | 增加设备维度分层 |
- 性能优化方案
案例:日活2亿的电商平台分流架构
graph LR
A[客户端请求] --> B{本地缓存分组?}
B -->|存在| C[直接返回分组]
B -->|不存在| D[服务端计算]
D --> E[分布式哈希集群]
E --> F[Redis缓存结果]
F --> C
C --> G[返回分组信息]
subgraph 优化策略
D -->|热点用户| H[布隆过滤器预处理]
E -->|批量计算| I[GPU加速哈希]
F --> J[TTL=24h]
end
性能指标:
缓存命中率:98.7%
计算延迟:<2ms (P99)
吞吐量:850,000 QPS
行业应用案例
案例1:视频平台推荐算法测试
问题:
用户分组后观看时长差异>20%(无理论依据)
次日留存率异常波动
根因分析:
# 原哈希函数
def faulty_hash(user_id):
return hash(user_id) % 1000 # Python内置hash不适用于分布式解决方案
替换为跨平台一致的MurmurHash3
增加用户活跃度的分层
引入桶内二次随机
效果
组间基线差异从$\(15%降至\)$ 1.2%
实验置信度提升了40%
案例2:金融风控AB测试事故
故障现象:
高风险用户集中出现在实验组
坏账率上升300%
技术分析
\[\text{用户ID} = \text{手机号} , \text{手机号段} \rightarrow \text{地域} \rightarrow \text{风险等级}\]改进措施
哈希前ID脱敏:hash(sha256(手机号)[:8] + salt)
增加风险等级维度分层
实时监控分组风险分布
3.4 AB测试的流程与步骤
ABtest其实就是控制变量法。为了评估测试和验证模型/项目的效果,在app/pc端设计出多个版本,在同一时间维度下,分别用组成相同/相似的群组去随机访问这些版本,记录下群组的用户体验数据和业务数据,最后评估不同方案的效果决定是否上线。
3.4.1 1.明确目标与假设
定义清晰的业务目标(如提升注册转化率、增加平均订单价值)。
提出具体的、可证伪的统计假设(\(H_0\)和\(H_1\))。
确定期望检测的最小有意义效应量MDE
3.4.2 2.确定目标指标与护栏指标
- 核心指标(Primary Metrics):直接反映实验目标的1-2个关键指标(如转化率、收入)
例如:修改购买页面的主色调能够帮助用户购买率提升3%
那么用户购买率就是我们关注的
还需要关注一些新策略是否会对其他重要指标产生负面影响
- 护栏指标(Guardrail Metrics):监控实验潜在负面影响的指标(如页面加载时间、关键功能使用率、崩溃率)。确保优化核心指标不以牺牲其他重要方面为代价。
Organization Guardrail Metrics:新功能可能好但是加载慢;该付款界面UI对用户的下单单价不能有影响
Trustworthy-related metrics:比如检查randomization,要用T-test或者卡方检验在查看A/B组的其他特征一致性
- 探索性指标(Exploratory Metrics):帮助理解用户行为变化,发现意外结果的辅助指标。
3.4.3 3.实验设计
单元选择(Unit of Diversion/randomization Unit):决定随机化的最小单元(用户ID,设备ID,会话ID,页面访问)。选择时需要考虑指标计算(用户级指标需用户级分流)、用户多次体验(保持体验一致性)、样本独立性(避免干扰)。用户级分流最常见。
分流比例(Traffic Allocation):分配多少样本去A/B组。通常是50:50,这样统计效率最高。但也会根据风险、流量大小调整(如90:10,新方案流量少)。需要确保样本量足够。
样本量计算(Sample Size Estimation):基于\(\alpha, \beta, MDE\),基准值(\(p_A\)或\(\sigma_A\))计算每组所需要的最小样本量/实验时长。这一点至关重要!样本不足会导致功效低(II类错误风险高),样本过大浪费资源和时间。
分层与区组(Sractification&Blocking):在随机化钱按重要特征(如国家、设备类型、用户新老)分层或区组,确保这些特征在组间均衡分布,提高统计精度(尤其当特征与指标强相关时)。
触发与曝光(Triggering&Exposure):明确那些用户会被纳入实验(所有的访问者?特定路径访问者?)。以及何时记录他们被“曝光”于实验条件、确保分析对象是真正“看到了”实验变化的用户,称为“曝光后分析”。
下面将具体举例进行介绍。
- WHO
AB实验实验需要控制变量,确保两组中只有一个不同的变量,其余变量一致。
必须满足的条件:
特征相同或相似的用户群组
同一时间维度
操作方法:
利用用户唯一标识的尾号或者其他标识进行分类,如奇偶分为两组
用一个hash函数将用户的唯一标识进行取模,分桶。可以将用户均匀地分到若干桶中,如分到100/1000个桶中,这样的好处就是可以进一步将用户打散,提高分组的效果。
当然,如果有多个分组并行的情况的话,要考虑独占域和分享域问题。独占域指不同域之间的用户相互独立,交集为空。对于共享域,我们要进行分层。但是在分层中,下一层要将上一层的用户打散,确保下一层用户的随机性。
实验对象:
如果是双边市场的话,可以从用户、平台、生产者三方进行实验
双边市场:指平台同时服务两类或多类相互依存的客户。例如,淘宝连接了买家和卖家,滴滴连接了乘客和司机,内容平台连接了用户和创作者。
信息流实验:指的是围绕“信息”在用户和生产者之间流动的过程所进行的实验。推荐系统是其中的核心组成部分。
用户(C端实验)
是最常见的AB实验场景,直接面向用户
产品策略:例如新功能上线,用户界面UI改版
运营策略:比如推送通知的文案、活动页面设计
客户端改版:例如APP的新版本、页面布局的调整
核心目标:提升用户体验,提高留存度和活跃度
cp/内容生产者(B端实验)
面向内容生产者或者商家的产品和策略
例如:内容池优化(让创作者更方便地上传内容)、创作者激励(新的分成机制)、黑产打击(识别和处理恶意内容)。
旨在提升B端的生产效率、积极性,维护平台生态健康
推荐实验(平台侧)
面对:链接用户和CP的关键桥梁—推荐算法
例子:自动训参(Auto-tuning,自动调整推荐算法的参数)、召回优化(提高找到用户可能喜欢的内容的效率)、排序优化(更好的对召回内容进行排序)、多目标优化(同时考虑点击率、停留市场、GMV等多个指标)、体验优化(减少广告干扰)、人群策略(针对特定人群提供定制化推荐)。推荐算法的效果直接影响着用户和CP两段的满意度。
推荐实验常用试验方法:(未展开,有机会可以展开)
ABTest
上线实验
MAB实验
在线寻参
人群圈选方式(行为圈选、标签圈选、属性圈选)
多层方案
分流:用户分流是指按照地域、性别、年龄等等将用户均匀地分成几个组,1个用户只能出现在1个组中。
适合互斥实验:实验在同一层拆分流量,且无论怎么拆分,不同组的流量是不会重叠的
例如“安卓用户”,“只看北京用户”。很多情况中不同城市的用户的的情况会有很大差别
问题:实际情况中,往往会上线多个实验。例如可能同时上线样式形态、广告位置策略、预估模型的实验。如果只按照分流模式来说,在每组实验放量10%的情况下,整体的流量只能同时开展10个实验。效率很低。为了解决这个问题,提出了用户分层、流量复用的方法。
分层:同一份流量可以分布在多个实验层,也就是说同一批用户可以出现在不同的实验层,前提是各个实验层之间无业务关联,保证这一批用户都均匀地分布到所有的实验层中,达到用户正交的效果就可以,从而让实验流量复用。
根据业务方人为定义一些分层–如:UI层、推荐算法层
每一层对用户随机分组:流量经过每一层时都会被打散重新分配,下一层的每一组的流量都随机来源于上一层各组的流量
实现同一个用户出现在不同层的不同组中,流量重复利用
分流分层模型:在此模型中增加组、层,并且可以相互嵌套。要求与实际的业务相匹配,拆分过多的结构可能会把简单的业务复杂化,拆分过少的结构又可能不满足实际业务。
上图就是分流分层模型的一个简单的图示。我们有:域1+域2=100%流量,B1层=B2层=B3层=域2流量,(B1-1)+(B1-2)+(B1-3)=B1层流量
规则:
域1和域2拆分流量,即域1域2互斥
流量流过域2中的B1层、B2层、B3层时,B1层、B2层、B3层的流量都与域2的流量相等,此时B1层、B2层、B3层的流量是正交的
流量流过域2中的B1层时,又把B1层分为了B1-1,B1-2,B1-3,此时B1-1,B1-2,B1-3又是互斥的
使用场景:
例1:B1层、B2层、B3层可能分别为:UI层、搜索结果层、广告结果层,这基层基本上没有业务关联,即使共用相同的流量(流量正交)也不会对实际的业务造成结果。
但是如果不同层之间所进行的实验相互关联,如B1层是修改的一个页面的按钮文字颜色,B2层时修改的按钮的颜色,当按钮文字颜色和文字颜色一样时,该按钮以及不可用了。因此建议同一类型的实验在同一层内进行,并且需要考虑到不同实验互相的依赖。
例2:域1的此种分流意义在于:如果我们希望其他任何实验都不能对我们的实验造成干扰,保证最后实验的可信度。
B端实验
内容池:
业务策略:低质过滤、热点运营、内容引入、内容使用天数
模型更新:tag更新、清晰度调整、封面图调整、评分体系更新
内容创作者:
业务策略:账号过滤、账号提权、账号引入、分润策略
模型更新:评级模型更新、黑产打击模型更新
what——选物料
明确改动点——话术模版/H5/图片素材,保证是单一因素
- where——选渠道
短信/外呼/邮件/站内私信
- when——选时机
立即出发/定时触达/例行触达/事件触发
注意:实验时长要与产品的“数据特征周期”一致
例如:直播类app产品,用户在周一到周五的活跃度较低,在周末活跃度高,以一个自然周为周期,不断循环。那么该产品的实验的时长应设置为一周。
How Large——决定样本量
在前面有介绍过具体公式,这里简化为\(N \approx \frac{16 \times \sigma^2}{\delta^2}\)
样本标准差\(\sigma\)衡量了整体样本数据的波动性
观测指标为绝对值类指标时:\(\sigma^2 = \frac{\sum_i^n(x_i-\bar{x})^2}{n-1}\)
观测指标为比率类指标时:\(\sigma^2 = p_A(1-p_A)+p_B(1-p_B)\),\(p_A,p_B\)为观测数据,比如希望点击率从20%提升到25%,那么\(p_A=0.2,p_B=0.25,\delta = 5%\)
组间预期差值\(\delta\)代表预期实验组和对照组两组数据的差
这里我们取\(\alpha = 0.05,\beta=0.2\),这里体现了AB实验的保守理念:低的\(\alpha\),尽量避免在\(H_0\)为真的时候拒绝它,;高的\(\beta\),可以适当的接受假的\(H_0\),也就是说改进实际游泳但是不采取;总结下来就是宁肯砍掉多个号的产品,也不应该让任何不好的产品上线。
Note为什么我们需要计算最小样本量?
理论上样本量肯定是越大越好。实际上,样本量是越小越好,因为
流量有限:小公司就这么点流量,还要精打细算做各种测试,开发各种产品。在保证样本分组不重叠的基础上,产品开发速度会大大降低。
试错成本大:如果拿50%的用户做实验,一周以后发现总收入下降了20%,这样一周时间的实验给公司造成了10%的损失,这样损失未免有点大。
所以也可以应用一个流量大小Trick——RAMP-UP PLAN or 灰度测试:初始阶段,先分配较少的流量(如1%)进入实验,初始实验如果一切正常, 进一步加大流量,初始实验如果出现异常, 随时可以终止实验
理论基础——CLT
当样本量足够大的时候,样本均值\(\bar{x}\)的分布近似服从正态分布。
当\(H_0\)为真的时候 ,实验组的样本均值\(\bar{x}\)服从均值为\(\mu_t = \mu_c\),方差为\(\frac{\sigma^2}{n}\)的正态分布。
标准化后的\(Z\)统计量:\(Z=\frac{\bar{x}-(\mu_c-\mu_t)}{\sqrt{2\sigma^2/n}}\)
第二类错误是指在H0为假的时候,我们错误地接受了H0,也就是说Z统计量落在了接受域内。
\[\beta = P(|\frac{\bar{x}}{\sqrt{2\sigma^2/n}}| \le Z_{\alpha/2}) = P(-Z_{\alpha/2} \le \frac{\bar{x} - (\mu_c - \mu_t)}{\sqrt{2\sigma^2/n}} \le Z_{\alpha/2})\]
由于中间部分服从标准正态分布,所以这个概率可以用正态分布的累计函数\(\Phi\)来表示:
\[\beta= \Phi(Z_{\alpha/2} - \frac{\mu_c - \mu_t}{\sqrt{2\sigma^2/n}}) - \Phi(-Z_{\alpha/2} - \frac{\mu_c - \mu_t}{\sqrt{2\sigma^2/n}})\] 不失一般性,我们假设\(\mu_c>\mu_t\)是一个比较大的整数,所以其中第二项\(\Phi(-Z_{\alpha/2} - \frac{\mu_c - \mu_t}{\sqrt{2\sigma^2/n}})\)的值会非常小,接近与0,因此可以忽略。与此同时,我们知道\(\beta = \Phi(-Z_{\beta})\),最终可以得到\[n \approx \frac{2(Z_{\alpha/2} + Z_\beta)^2 \sigma^2}{(\mu_c - \mu_t)^2}\]。其中\(\delta = |\mu_t-\mu_c|\)是我们希望检测到的最小可检测效应MDE。\(\sigma^2\)是指标的方差,通常需要预估或者根据历史数据计算。
以上公式是计算出单个实验组所需的样本量,若有多个实验组,乘以实验组的个数就可以得到最终的样本量;样本量也可以是一段时间里累计的样本量,比如需要10000个样本,每天1000个,累计10天也是可以的。
举例:
对于绝对值指标:
- 某商品详情页平均停留时长的标准差是20s,优化了商品详情页面后,预估至少有5s的提升,AB测试每个组需要的最少样本量:\(\sigma = 20,\delta=5\),每个组所需要的最少的样本量就是16*202/52=256
比率类指标:
- 某商品详情页点击率20%,优化后预期点击率提升到25%,每个组需要的最少样本量:16(0.20.8+0.25*0.75)/(0.25-0.2)**2
在线计算工具:Evans awesome AB Tools
代码(基于\(delta\) \(method\)):\(\sqrt{n}(g(Y_n) - g(\theta)) \xrightarrow{d} N(0, \sigma^2 g'(\theta)^2)\)
import numpy as np
import math
from sklearn.linear_model import MultiTaskLasso, Lasso
import pandas as pd
import scipy.stats
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler- 用卡方检验检验分流的均匀性
x 和 y:通常代表实验组和对照组的用户总数(或流量总数)。代码中的 31188, 31188 表示两组的流量是相等的。
x_target 和 y_target:通常代表实验组和对照组中某个特定事件的发生次数,例如转化、点击等。代码中的 3461, 3423 是两组的转化次数。
如果p-value非常小(比如小于0.05),说明两组的流量分布存在显著差异,可能分流有问题,实验结果不可信。
from scipy.stats import chi2_contingency
def chi_test(x,y,x_target,y_target):
kf_data = np.array([[x,x_target], [y,y_target]])
kf = chi2_contingency(kf_data)
print('chi-sq=%.4f, p-value=%.4f, df=%i expected_frep=%s'%kf)
chi_test(31188,31188,3461,3423)chi-sq=0.1780, p-value=0.6731, df=1 expected_frep=[[31205.1115218 3443.8884782]
[31170.8884782 3440.1115218]]- 德尔塔方法计算方差
计算两个随机变量之比的方差。在ABTest中,CTR = 点击数/曝光数,CVR = 转化数/点击数,这两个指标本质上都是两个随机变量的商。
问题背景:传统的二项分布方差公式适用于伯努利试验(例如每个用户点击或者不点击)。但是对于比率指标,分母本身也是一个随机变量。这时使用简单的二项分布公式来估算方差就不正确了。
推导:假设我们需要计算\(R = Y/X\)的方差。通过一阶泰勒展开近似,得到\(Var(\hat{R}) = Var\left(\frac{\bar{Y}}{\bar{X}}\right) \approx \left(\frac{\partial g}{\partial x}\right)^2 Var(\bar{X}) + \left(\frac{\partial g}{\partial y}\right)^2 Var(\bar{Y}) + 2\left(\frac{\partial g}{\partial x}\right)\left(\frac{\partial g}{\partial y}\right)Cov(\bar{X}, \bar{Y})\),其中\(g(x,y) = \frac{y}{x}, \frac{\partial g}{\partial x} = -\frac{y}{x^2}, \frac{\partial g}{\partial y} = \frac{1}{x}\),代入得到\(\Rightarrow Var(\hat{R}) \approx \frac{E[Y]^2}{E[X]^4} Var(\bar{X}) + \frac{1}{E[X]^2} Var(\bar{Y}) - \frac{2E[Y]}{E[X]^3} Cov(\bar{X}, \bar{Y})\)
def var_dtm(y_mean, x_mean, var_y, var_x, xy_mean):
#计算协方差
def cova(x_mean,y_mean,xy_mean):
return xy_mean-x_mean*y_mean
covar = cova(x_mean,y_mean,xy_mean)
#商的variance
var_ratio = var_y/x_mean**2 + var_x*y_mean**2/x_mean**4 - 2*covar*y_mean/x_mean**3
return var_ratio
#发布器头图的 曝光数 > 发布数 为例
var = var_dtm(y_mean = 0.035214194, x_mean = 2.794877088302219
,var_y = 0.073726526, var_x = 185.240175
, xy_mean = 0.410843231521)
#实际的方差 有可能比二项分布折算方差会大很多
print('二项方差:',round(0.012599/(1-0.012599),4))二项方差: 0.0128print('实际方差:',round(var,4))实际方差: 0.0122- 估算样本量
'''
mean:对照组指标的均值(如基准转化率)
var:指标的方差,代码在调用时会分别使用“二项分布方差”和“德尔塔方法方差”。
lift_rate:预期的最小可检测效应\delta
''''\nmean:对照组指标的均值(如基准转化率)\nvar:指标的方差,代码在调用时会分别使用“二项分布方差”和“德尔塔方法方差”。\nlift_rate:预期的最小可检测效应\\delta\n'def sample_size(mean = 0.01259955,var = 0.0122,lift_rate = 0.025,alpha = 0.05,beta = 0.2):
import math
lift = lift_rate * mean
num = var*(scipy.stats.norm.ppf(1-alpha)+scipy.stats.norm.ppf(1-beta))**2/(lift**2)
return math.ceil(num)
print('采用二项方差的样本量估计:', sample_size(var = 0.0128))采用二项方差的样本量估计: 797606print('采用deltaMethod的样本量估计:',sample_size())采用deltaMethod的样本量估计: 7602183.4.4 4.实施与随机化,数据收集与监控
开发并部署实验变体(B)
- 创建变体:对网站原有版本的元素进行所需要更改。可能是更改颜色,交换页面上元素是顺序,隐藏导航元素或完全自定义的内容。
构建可靠的随机化引擎,确保分配是真正的随机且不可预测的。常用方法:用户ID哈希取模、伪随机数生成器(需要确保seed独立)。
记录分配日志(用户ID,时间戳、分配组、实验ID)(埋点)
- 这里要注意辛普森悖论!要严格执行之前设计的分流分层方案让样本均匀随机。
收集核心指标、护栏指标、探索性指标的数据(埋点采集数据)
实时/准实时监控:
样本量积累情况
- 比如实验组和对照组的分流的流量是否均匀
核心指标的点估计和置信区间变化
护栏指标是否有异常波动(设置警报阈值)
检查AA测试是否通过
观察对于用户的行为埋点是否埋的正确
3.4.5 5.数据分析
数据准备:清洗数据,处理异常值,确认分析窗口(如实验开始后稳定期的数据)。
AA测试/平衡检验:在分析AB结果之前,先检查实验组(A)和对照组(A)在已知不受实验影响的指标上(如实验前历史数据、用户属性、分流前行为)是否存在显著差异。若显著,表明随机化可能失败或者数据有问题,需要排查。
效应估计:计算核心指标的组间差异\(\bar{y}_B-\bar{y}_A\)或者\(\hat{p}_B-\hat{p}_A\)
统计显著性差异:使用合适的检验方法(t检验、Z检验、回归)计算P值
| 指标类型 | 检验方法 | 公式 | 适用场景 |
|---|---|---|---|
| 连续型指标 (人均时长、客单价) |
双样本t检验 | \(t = \frac{\bar{Y}_A - \bar{Y}_B}{\sqrt{\frac{s_A^2}{n_A} + \frac{s_B^2}{n_B}}}\) \(df \approx \frac{(\frac{s_A^2}{n_A} + \frac{s_B^2}{n_B})^2}{\frac{(\frac{s_A^2}{n_A})^2}{n_A-1} + \frac{(\frac{s_B^2}{n_B})^2}{n_B-1}}\) |
收入、时长等平滑分布数据 |
| 比例型指标 (转化率、点击率) |
双样本Z检验 | \(Z = \frac{\hat{p}_A - \hat{p}_B}{\sqrt{\hat{p}(1-\hat{p})(\frac{1}{n_A} + \frac{1}{n_B})}}\) \(\hat{p} = \frac{X_A + X_B}{n_A + n_B}\) |
转化率、留存率等二分类数据 |
| 计数型指标 (人均点击次数) |
负二项回归 (处理过离散) |
\(\log(\mu_i) = \beta_0 + \beta_1 \cdot \text{Treatment}_i\) \(\text{Var}(Y_i) = \mu_i + \alpha\mu_i^2\) |
用户行为次数(方差>均值) |
Q:为什么转化率、点击率是二分类的数据?
A:然我们常把转化率、点击率表述为百分比(如5.2%),但它们的底层数据本质是二分类数据(Binary Data)。原因在于构成这些指标的每一个最小观察单元只有两种互斥状态:
点击率CTR点击次数/曝光次数:点击记录为1,不点击记录为0
转化率CVR注册次数/进入落地页人数:注册记录为1,不点击记录为0
二分类数据违背连续型检验的核心假设:
假设 连续型变量 二分类数据 数据分布 近似正态分布 Bournulli分布(0-1分布) 方差稳定性 方差与均值无关 方差依赖均值$p(1-p)$ 数值范围 无边界限制 数值被压缩在[0,1] 案例:广告点击率AB测试 (A组 vs B组)
A组:曝光 10,000 次 → 点击 600 次 → \(\hat{p}_A = 0.06\)
B组:曝光 10,000 次 → 点击 750 次 → \(\hat{p}_B = 0.075\)
若错误使用t检验:
计算两组的点击率(0.06vs0.075)的t统计量,得出p<0.05
问题:忽略数据的本质是离散二分类,且方差p(1-p)在p=0.5时最大,导致检验失真
正确使用Z检验:
\(Z = \frac{\hat{p}_B - \hat{p}_A}{\sqrt{\hat{p}(1-\hat{p}) \left( \frac{1}{n_A} + \frac{1}{n_B} \right)}}, \quad \hat{p} = \frac{600+750}{10000+10000} = 0.0675\)
得到Z=5.0,p<0.000,结论可靠
Q:什么时候可以近似使用t检验?
A:当同时满足以下两个条件时,二分类数据近似生态分布,可以谨慎使用t检验
样本量足够大:\(n \cdot p >5\)且\(c\cdot(1-p)>5\)
比例值远离边界:\(0.2<p<0.8\),避免p接近0或1导致分布高度偏态
当然,互联网场景中,转化率等常不满足,严格使用比例检验或逻辑回归。
CI构建:计算效应量的CI
多重检验校正:如果同时考虑多个核心指标或者同一个指标的多个变体(A/B/n测试),需要进行校正,以控制整体错误发现率(FDR)或族系错误率(FWER)。容易忽视但是很重要!
效应量解读:结合实际业务解读统计学差异是否显著。一个统计学上显著但是效应量微小的结果可能没有实际意义。
3.4.6 6.决策
显著且正向:发布B方案
显著但负向:放弃B,分析原因
不显著:
检查功效:样本量是否足够?效应量是否小于MDE?
检查实验设计:随机化是否有效?指标定义是否合理?触发逻辑是否正确?
结论:在当前条件下,未检测到B方案与A方案有统计显著差异。这不等于证明两者效果相同(可能是II类错误)。
考虑结果在实际流量下的稳健性(如网络效应、长期效应)
Q:如果你发现你在AB测试当中所选取的指标在统计上来说都是不显著的,你该怎么去判断这个实验的收益?
A:
在当前条件下,未检测到B方案与A方案有统计显著差异。这不等于证明两者效果相同(可能是II类错误)
但进一步,我们可以将这个指标去拆分成每一天去观察,如果指标的变化曲线每一天实验组都高于对照组,即使他在统计上来说是不显著的,我们也认为在这一个观测周期内,实验组的关键指标表现是优于对照组,并得出优化上线的结论。
Q:如果你在AB测试中发现实验组核心指标明显优于对照组,那这个优化就一定能够上线吗?
A:
不一定。举个例子,比如说有的时候我们想要提升产品的视觉展现效果。但是这种优化可能是以用户等待内容展现的时间作为代价来进行提升的。所以一个方面的优化可能会导致另一个方面的劣化。在做这个优化的时候,可能会对其他部门产生一些负向的影响,进而导致公司收入的下降。
所以,我们在进行AB测试的时候,必须要综合评估所有方面的一些指标变动,同时对于收益和损失来做一个评估,才能确认这个优化可以最终上线。
3.5 挑战与陷阱
其实常见的错误总得来说就是两类,一类是弃真,一类是存伪。
弃真是指实验组和对照组没有显著差异,但是我们接受了新方案。减少这种错误的方法就是提高显著性水平\(\alpha\),比如p小于0.05才算显著,而不是选用0.1 存伪是指实验组和对照组有显著差异,但是我们没有接受新方案。这是第II类错误。
3.5.1 新奇效应(Novelty Effect)/首因效应(Primacy Effect)
用户对新方案B的暂时性好奇或抵触导致行为短期偏离长期趋势。
量化公式
首因效应强度 = \(\frac{\text{老用户实验组留存率} - \text{老用户对照组留存率}}{\text{新用户实验组留存率} - \text{新用户对照组留存率}}\) (比值>1.3表示显著存在)
新奇效应衰减率 = \(1 - \frac{\text{实验组第7日DAU}}{\text{实验组第2日DAU}}\) (衰减率>40%需警惕)
解决方案:延长实验时间观察指标是否稳定;考虑仅对新用户实验
实验设计阶段
将用户分为 认知锚点人群(老用户)和 无锚点人群(新用户)
对新用户设置 学习期(前3天数据仅监控不分析)
数据分析阶段
def adjust_novelty_effect(data):
# 剔除前3天的新奇效应数据
adjusted_data = data[data['day'] > 3]
# 计算首因效应修正因子 (基于老用户衰减曲线)
primacy_factor = fit_decay_curve(old_user_data)
return adjusted_data * primacy_factor决策阶段:
若首因效应主导,需教育用户(如添加新功能引导教程)
若新奇效应主导,关注长期留存曲线(看第30天留存率)
例如:“当实验组在第4周留存率比对照组高5%,即使首周数据差也值得发布”
NoteQ:对于一个新功能实施了ABtest,发现新功能效果 更好,但是一周之后效果迅速下降。
A:新奇效应,效果消失后重复使用减少
3.5.2 样本比例不平衡(Sample Ratio Mismatch - SRM)
实际分配的人数比例与设计比例(例如50:50)存在显著偏差。严重!
可能的原因:
随机化算法bug
数据管道问题
用户重复计数
实验配置错误
错误的例子:
实验中,在不同渠道/应用市场中,发布不同版本的APP/页面,并把用户数据进行对比
简单地从总体流量中抽取n%用于实验,不考虑流量分布,不做分流处理
不同应用市场渠道的用户常常带有自己的典型特征,用户分布具有明显区别。对总流量进行简单粗暴地抽样也有着同样的问题——分流到实验组和对照组的流量可能存在很大的分布差异。
AB测试要求我们尽可能地保持实验组和对照组的流量分布一致,与总流量也需分布一致,否则得出的实验数据不具有可信度。
必须解决SRM才能分析结果!
3.5.3 辛普森悖论(Simpson’s Paradox)
在子群体中观察到的趋势与合并数据中的趋势相反。
3.5.4 相关实验的相互影响
前面有讲到,相关性实验放到同一层,不相关的实验可以放在不同层。比如按钮红色or蓝色VS按钮圆形or方形是相关的实验,用户将收到“按钮颜色Red”以及“按钮形状Round”两个策略的影响。
graph TD
U[用户] -->|同时经历| E1[颜色实验]
U -->|同时经历| E2[形状实验]
E1 -->|红色/蓝色| D[点击行为]
E2 -->|圆形/方形| D
D -->|混杂结果| R[无法区分影响因素]
这样我们就无法判断究竟是哪个策略影响了该用户的行为。换句话说,由于两个实验存在关联,用户重复被实验命中,实验结果实际收到了多个策略的影响。这种情况下,两个实验的结果便不再可信了。
- 传统正交分层(适合不相关实验)
| 用户ID | 层1: 按钮颜色 | 层2: 推荐算法 |
|---|---|---|
| 1001 | 蓝色 | 算法A |
| 1002 | 红色 | 算法B |
| 1003 | 蓝色 | 算法A |
- 因子设计(2×2实验,解决相关问题)
| 用户ID | 颜色+形状组合 | 效果评估 |
|---|---|---|
| 1001 | 蓝色 + 方形 | 转化率X% |
| 1002 | 蓝色 + 圆形 | 转化率Y% |
| 1003 | 红色 + 方形 | 转化率Z% |
| 1004 | 红色 + 圆形 | 转化率W% |
- 数据分析结果:
| 组合方案 | 用户数 | 转化率 | 平均订单额 |
|---|---|---|---|
| 蓝色方形 | 10000 | 5.2% | $128 |
| 蓝色圆形 | 10000 | 6.1% | $135 |
| 红色方形 | 10000 | 5.8% | $132 |
| 红色圆形 | 10000 | 7.5% | $145 |
- 效应计算
import numpy as np
# 定义各组转化率
blue_square = 0.052
blue_circle = 0.061
red_square = 0.058
red_circle = 0.075
# 计算主效应和交互效应
color_effect = ((red_square + red_circle) - (blue_square + blue_circle)) / 2
shape_effect = ((blue_circle + red_circle) - (blue_square + red_square)) / 2
interaction = ((red_circle - red_square) - (blue_circle - blue_square)) / 2
print(f"颜色主效应: {color_effect:.4f}") # 0.0100颜色主效应: 0.0100print(f"形状主效应: {shape_effect:.4f}") # 0.0130形状主效应: 0.0130print(f"交互效应: {interaction:.4f}") # 0.0040交互效应: 0.0040- 适用场景
| 场景类型 | 案例 | 推荐设计 |
|---|---|---|
| UI元素交互 | 按钮形状+颜色+文案 | 2*2*2因子设计 |
| 定价策略组合 | 基础价+折扣+运费策略 | 三因子混合设计 |
| 产品功能叠加 | 搜索+筛选+排序功能优化 | 分阶段因子设计 |
| 营销组合策略 | 渠道+文案+优惠券类型 | 正交分层+因子设计 |
实施注意事项:
四组实验需要四倍于单实验的样本量
正交互效应是策略相互增强,负交互效应是策略相互抵消
业务优先级:
当交互效应>主效应时,必须采用组合策略
当主效应>>交互效应时,可以独立优化
实验平台支持:
class FactorialExperiment: def __init__(self, factors): self.factors = factors # 如 {'颜色': ['蓝','红'], '形状': ['方','圆']} self.groups = self._generate_groups() def _generate_groups(self): """生成所有因子组合""" from itertools import product return list(product(*self.factors.values())) def assign_user(self, user_id): """分配用户到特定组合""" hash_val = hash(user_id) % 100 group_size = 100 / len(self.groups) group_idx = int(hash_val // group_size) return self.groups[group_idx]
黄金法则:当实验策略影响用户的同一决策时刻或同一认知维度时,必须使用因子设计而非正交分层。
3.5.5 稀释效应(Dilution Effect)
指不符合实验触发条件的用户(如从未访问过实验页面的用户纳入分析),稀释了真实效应。
解决方案:
- 采用“仅曝光用户分析”或“触发用户分析”
3.5.6 干扰(Interference)
一个用户的体验/行为收到其他用户所在组的影响(如社交功能)。违背了SUTVA(稳定单位处理值假设)。
网络效应(Networking Effect)控制组的用户会被实验组的用户影响
例如:
我们对司机的激励策略,司机群里会讨论所以会感觉自己受到了不公平的待遇
假设好友被分到了实验组,我被分到了对照组。曝光给好友的内容更加的有吸引力,他作出了点赞、评论等互动行为。而产品的社交属性,使我可以看到好友的互动行为,原本不会被曝光给我的内容,我通过好友的互动间接接收到了。也提高了我去互动的概率,提高了活跃程度。这样就发生了实验组想对照组溢出的问题,独立的假设受到了破坏。
直播pk体验中,pk组的体验组连线对战组
解决方案:用户聚类:按用户的关联度将用户聚成cu,保证簇内用户的关联强,而簇间的关联弱,那么簇与簇之间是近似独立的
- 假如一个用户被划分到对照组中,那么大部分与他直接联系的用户也应该被划分到对照组中。
Two_sided markets实验组和对照组会竞争一样的资源
当领券的用户需求增加,会获得更多的司机资源,从而让没领券的对照组可用的司机资源减少了!
如果在一个地理区域中划分实验组和对照组,验证一个乘客端的优化。如果实验组的优化带来了需求的提升,那就会有更多的司机接到了来自实验组的订单。短时间内司机的数量固定,分配给实验组的司机多了,自然对照组的司机就少了。导致实验组结果高估,且破坏了独立假设。
解决方案:系统控制干预,
地理分离:从地理上区隔用户,这种情况适合打车平台这种能从地理上区隔的,比如北京作为实验组,上海作为对照组,需要两个城市的样本量相近。
时间分离:只有在effect短的时候(比如打车)才有用,但长时间(比如是否会推荐给其他用户)就没用
解决方案:核心是系统控制干预,降低对照组用户(没上策略的用户)接触到待评估功能的几率
以更大粒度(群组/网络)随机化
使用聚类标准误
设计特殊实验
- 时间片轮转实验:是一种处理个体之间相互干扰的实验方法,在一定的实验对象上 进行实验组策略和对照组策略上的反复切换。比如快手直播PK:让用户无法知晓下一个时间是否是实验组
3.5.7 统计显著\(\neq\)实际显著
Q:如果发现AB测试的结果在统计上显著,但是在实际中不显著,这是为什么?
A: 统计学上的显著并不意味着实际效果的显著,假说检验只是告诉我们数据差异由随机产生的概率多大,而实际显著是一个业务对改进商业价值的业务判断。
比如,我们做了一个改动让APP的启动时间的优化了0.001秒,这个数字可能在统计学上对应的P值很小——统计学显著,但是在实际中用户0.01秒的差异是感知不出来的。那么这样一个显著的统计差别,其实是没有商业意义的。
造成这个结果可能的原因是我们在AB测试当中所选取的样本量过大(比如样本量分母的Minimum detectable effect太小了),导致样本和总体数据量差异很小,这样的话即使我们发现一个细微的差别,它在统计上来说是显著的,但对实际应用来说是不显著的。
解决方法就是我们要设定一个合理的Minimum detectable effect,并根据它计算最小样本量。
3.5.8 多重检验问题(Multiple Testing Problem)
同时检验多个假设或多次查看数据(peeking)会大大增加整体I类错误。
graph TD
A[开始实验] --> B[第3天查看结果]
B --> C{结果显著?}
C -->|是| D[提前终止]
C -->|否| E[继续实验]
D --> F[虚假结论]
E --> B
例如,有三个组,有一个组p-value<0.05,也不能执行,因为此时:
Pr(no false positive) = (1 - 0.05) ^3 = 0.857
Pr(at least 1 false positive) = 1 - 0.857 = 0.143
Type I error rate over 14%
例如
解决方案:
预先实验周期计算
- 完整周期公式:\(T = max(7, \frac{n}{N_{\text{daily}}} ) \times \text{季节因子}\),\(n\) = 基于MDE计算的样本量,\(N_{\tet{daily}}\) = 日均可用流量,季节因子 = 1.2(促销季)或 0.8(淡季)
使用序贯检验或贝叶斯方法处理peeking
# 序贯检验
# O'Brien-Fleming边界示例
def obrien_fleming_bound(alpha, t, T):
""" t:当前信息分数, T:计划总信息量 """
z = stats.norm.ppf(1 - alpha/2)
return z * np.sqrt(T / t)
# 第50%进度时边界:z*√2 ≈ 1.414z (比固定检验更严格)
# 贝叶斯方法
def should_stop(prior, data_A, data_B):
posterior = update_posterior(prior, data_A, data_B)
prob_better = (posterior['B'] > posterior['A']).mean()
return prob_better > 0.95 or prob_better < 0.05- 对结果进行多重检验校正
真实案例:电商大促按钮测试
实验设定:
目标:测试购物车按钮颜色(红VS蓝)
预定周期:14天(覆盖两个完整周末)
每日流量:100,000用户
Data Peeking导致的错误决策:
| 实验日 | 操作 | 观测结果 | 实际最终结果 |
|---|---|---|---|
| 第3天 | 查看数据并终止 | “红色胜出12%” | 虚假结论 |
| 第7天 | 查看数据并继续 | “无差异” | - |
| 第14天 | 完整数据分析 | “蓝色胜出2%” | 真实结论 |
- 损失评估:\(\text{机会成本} = 7\text{天} \times 100\text{K用户/天} \times 2\% \times \text{客单价} = \$140,000\)
3.5.9 长期效应(Long-term Effects)
AB测试通常运行几天到几周,可能无法捕捉方案的长期影响(如用户疲劳、生态变化)。
解决方案:
结合长期跟踪研究
使用“保留组”进行长期观察
3.5.10 方差估计问题
这一点在前面也有提到。用户级指标常常存在用户内行为相关性(非独立),导致传统方差估计低估。
解决方法:使用Delta方法、自助法(Bootstrap)、或基于用户聚类的标准误(Cluster-Robust Standard Errors)。对用户级分流尤其关键!
3.5.11 外部环境带来偶然因素
下雨天打车、大促时电商
3.5.12 单侧检验
当显著性水平一定时,如要在多个选件中确定入选者,那么单侧检验所需观察到的选件之间的转化率差异更小。这似乎很有吸引力,因为与使用双侧检验相比,单侧检验可以更早地确定入选者。但单侧检验是有代价的!
例如,在一个单侧检验中,测试B是否比A好必须在开始测试之前,决定是测试 B 优于 A 还是 A 优于B。但是,如果是先查看了 A/B 测试的结果并看到 B 优于 A,然后决定进行一个单侧检验来看这种差异是否具有统计意义,那么就违反了统计测试背后的假设。违反测试的假设意味着您的置信区间不可靠,并且测试的误报率比预期的要高。
您可以将单侧检验看做是一种已经由裁判做出决定、只是对该选件进行试验的测试。在单侧检验中,您已经确定了入选选件,而且只是想证明这一点,而不是向每个体验提供平等的机会来证明自己可以是入选者。单侧检验只应在这种极少发生的情况下使用:您只关注某个策略是否优于其他策略,而不是其他策略优于某个策略。
避免出现单侧检验问题,我们通常使用始终运用双侧检验的 A/B 测试解决方案!
3.5.13 贝叶斯AB测试(Bayesian AB Testing)
待补充
3.5.14 序贯检验(Sequential Testing)
允许在实验运行过程 中多次查看数据并可能提前停止实验(当结果足够显著或明显无效时)
能控制整体I类错误率(如使用序贯概率比检验——SPRT,Alpha Spending Functions)
提高实验效率(尤其当效应很大或很小),减少资源浪费
3.5.15 A/B/n Tesing & 多臂老虎机(Multi-armed Bandit - MAB)
A/B/n:同时测试多个变体(A/B/C/D…)。需要多重检验校正
MAB:一种在线学习算法,在探索(收集信息)和利用(选择当前最优)之间动态平衡流量分配。适用于需要持续优化且快速反馈的场景(如广告竞价)。牺牲严格的因果推断换取更快的收益提升。
3.6 AA实验
AA测试(A/A Test)是实验系统中的”校准工具”,指在相同策略下将用户随机分为两个或多个组进行比较,确保实验系统本身的可靠性。AA实验通常用来辅助观察指标在产品不做改变时的偏差范围。我们通常会在实验里加一个和对照组一模一样的实验组来观察这个偏差,而如果这个偏差很大,通常你的AB实验也容易结果不置信。
为什么业务必须做AA测试?
graph TD
A[业务决策依赖AB测试] --> B{实验系统可信吗?}
B -->|AA测试通过| C[可靠决策]
B -->|AA测试失败| D[错误决策链]
D --> E[上线无效方案]
D --> F[放弃有效方案]
作用有哪些呢?
实验平台验证:检测分流系统是否真的随机
指标敏感性校准:确定业务指标的天然波动范围
统计方法检验:验证分析模型是否产生假阳性
数据管道审计:发现埋点采集或者ETL处理错误
案例:某电商平台AA测试发现“凌晨用户转化率虚高3%”,根源是因为爬虫浏览量未过滤
AA测试的起因是什么呢?
做AB实验的时候,有时尽管我们发现AB两组出现了明显差异,但我们依旧无法确认这种差异是实验条件不同带来的,还是AB两组用户本身的差异带来的。有时候,即便采用特别均匀的哈希打散算法,同时扩大样本量,也依然会出现AB两组用户在空跑期(AB两组用户实验条件一致),差异显著的情况。
因此,为了规避这个问题。很多企业采用了AA测试(空跑期)方法——正式开启实验之前,先进行一段时间的空跑,对AB两组用户采用同样的实验条件,一段时间后,再看两组之间的差异。
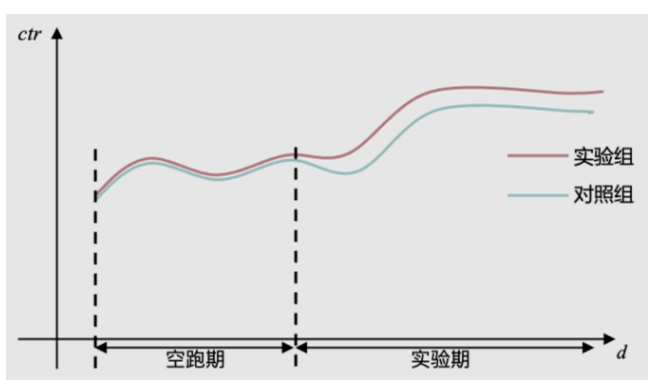
如果差异显著,数据弃之不用,重新选组。
如果差异不显著,记录两组之间的均值差,然后在实验期(AB两组实验条件不同)结束时,用实验期的组间差异,减去空跑期的组间差异,得到一个净增长率。
这种方式的问题是:对绝大多数APP来说,用户留存率不是100%。这意味着今天活跃的用户,明天可能就不来了。因此,今天按照一定规则圈定的用户群,到明天就不是同一拨人了。换句话说,即便空跑期的AA实验发现两组没有差异,等到进行AB实验时,两个实验组里的用户早就不同了。你也没法确定,AB两组用户本身没有差异。
还有些企业,会直接开三组流量,对照组、实验组、AA对照组。通过对比对照组和AA对照组,来判断实验组的固有差异。但这种方式更加不能确定对照组和实验组之间的固有差异,是更加不靠谱的方式。
那么,如果AA测试没有用,那我们该如何规避组间固有差异带来的问题呢?
3.6.1 AA波动比率
既然组间差异一定存在,那我们不妨接受这个前提,并且用统计方式来衡量差异大小,在计算实验效果的时候,把差异考虑在内即可。
举个例子,假如我们随机抽取2N个用户分为两组(每组N个),做一次实验,并进行指标对比。那么我们可以计算出两组用户在给定\(\alpha\)值下,指标差异的置信区间。
我们可以把置信区间归一化,得到围绕样本均值波动的比率(给定\(\alpha\)水平下)。这个波动比率,可以认为是任意两次随机分组,在给定\(\alpha\)水平下的指标固有差异。
接下来,我们可以判断,如果AB实验得出的效果(改进比率),小于波动比率,那很可能只是正常误差,这个实验结论是不靠谱的。相反,如果实验效果大于波动比率,意味着这个实验结论是值得信赖的。
针对不同的指标、\(\alpha\)水平、时间、样本数量(一般选常用AB实验的用户数量,便于参照),我们可以计算出AA波动率的表,通过这种方式,我们就把传统的AA实验,转换为了AA波动。用量化的方式,描述了组间固有差异!
操作步骤:
先对 各种关键指标,分别做常用用户数量下的AA波动范围图
配置每个实验的时候,直接进行AB测试,不考虑AA
分析数据结果的时候,考虑AB之间的差异,要大于AA差异
3.6.2 AA测试的统计学原理
假说检验
\(H_0\):对照组A2与实验组A1没有差异
\(H_1\):A1与A2存在显著差异
在理想系统中:\(P(\text{拒绝}H_0 | H_0\text{为真}) \leq \alpha \quad (\alpha=0.05)\)
判定三要素
| 维度 | 健康标准 | 检测方法 |
|---|---|---|
| 样本比例 | \(\chi^2\)检验\(p>0.05\) | \(\chi^2=\sum\frac{(O-E)^2}{E}\) |
| 核心指标 | t检验\(p>0.05\) | \(t = \frac{\bar{Y}{A1} - \bar{Y}{A2}}{s_p\sqrt{2/n}}\) |
| 用户特征分布 | KL散度<0.05 | \(D_{KL}(P_{A1}\parallel P_{A2})\) |
3.6.3 业务落地的实施框架
执行频率策略
| 业务阶段 | 频率 | 样本量 | 特别关注 |
|---|---|---|---|
| 新实验平台上线 | 连续20次 | 10万用户/组 | 分流算法一致性 |
| 常规运营期 | 每月一次 | 业务日均UV的20% | 指标波动基线 |
| 重大升级后 | 立即执行 | 等同AB测试规模 | 数据管道完整性 |
典型业务场景配置
class AATestConfig:
def __init__(self, business_type):
self.metrics = self._get_core_metrics(business_type)
self.duration = self._calculate_duration()
def _get_core_metrics(self, business_type):
# 不同业务的核心监控指标
config = {
"ecommerce": ["转化率", "客单价", "加购率"],
"fintech": ["申请通过率", "坏账率", "放款时效"],
"content": ["CTR", "观看时长", "分享率"]
}
return config.get(business_type, ["DAU"])
def _calculate_duration(self):
""" 覆盖完整业务周期 """
base_days = 7 # 至少1周
if "fintech" in self.metrics:
return max(base_days, 30) # 金融需完整账期
return base_days实施流程图解
graph TB
S[启动AA测试] --> A{样本比例健康?<br>χ² p>0.05}
A -->|否| B[警报:分流故障]
A -->|是| C{核心指标差异?<br>t检验 p>0.05}
C -->|否| D[警报:指标异常]
C -->|是| E{用户特征均衡?<br>KL<0.05}
E -->|否| F[警报:样本污染]
E -->|是| G[系统认证通过]
classDef red fill:#ffe6e6,stroke:#ff6666;
classDef green fill:#e6ffe6,stroke:#66cc66;
class B,D,F red
class G green
3.6.4 业务场景实战案例
案例1:金融风控系统AA测试失败
背景:某消费贷平台AB测试结果波动异常
AA测试发现
申请通过率差异p=0.03(预期应无差异)
用户年龄分布KL=0.18(显著不均衡)
根因定位
graph LR
A[分流不均] --> B[用户ID哈希冲突]
B --> C[年轻用户集中到A组]
C --> D[通过率虚高]
解决方案
将哈希算法从MD5迁移至SHA-256
增加bucket数量至1000(原本是100)
添加年龄维度均衡检查
案例2:视频平台指标波动基线建立
业务需求:判断+1%观看时长提升是否显著
AA测试输出:\(\sigma_{\text{时长}} = 0.8\% \quad (\text{95%波动区间} [-1.6\%, +1.6\%])\)
决策规则
提升<1.6%,可能为自然波动
提升>1.6%,可判定为显著效果
3.6.5 高级业务应用模式
多维度AA测试矩阵
| 维度 | 检测目标 | 业务意义 |
|---|---|---|
| 时间切片 | 周末vs工作日波动 | 活动效果评估参考 |
| 地理维度 | 区域间天然差异 | 地域策略实验校准 |
| 用户分层 | 新老用户行为基线 | 个性化策略实验基础 |
| 设备类型 | ios/Android差异 | 跨平台实验可比性保障 |
动态基线系统架构
graph LR
A[实时数据流] --> B{是否AA测试期}
B -->|是| C[计算指标差异]
C --> D[更新波动基线]
D --> E[存储至基线库]
B -->|否| F[对比当前AB测试与基线]
F --> G{超出基线范围?}
G -->|是| H[触发警报]
G -->|否| I[正常输出结果]
3.7 ABTest的局限性
Q:如果一个人有多个账号,分别做不同用途,abtest的时候怎么分组才最合理呢?
A:我们对这类人的分类是,看的不是他是谁,而是他做了什么。按照我们对行业的分类,行为不同的话就是两类人,和身份证是不是同一个无关。我们要聚合的是有相同行为特征的账户,而不是人。
用户角度:一部分用户无法使用某类功能而另一类用户则可以,可能会引发舆情问题
开发角度:同时维护多套代码也有一定成本。这就导致我们无法直接使用AB实验
伦理上不可行:比如探究社交压力对用户发表朋友圈的意愿有什么影响,不可能在用户朋友圈伪造或隐藏点赞和评论。
成本问题:需要足量随机流量使结果具备统计意义,会耗费流量;需要持续一段时间以收集数据,耗费时间;当可做A/BTest的选择太多时,往往难以全部尝试。